
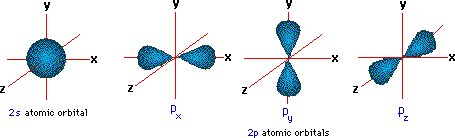

As for a molecular system, I think it is best if i left that to someone else. Electrons in the same subshell have the same energy, while electrons in different shells or subshells have different energies. Electron shells consist of one or more subshells, and subshells consist of one or more atomic orbitals. These additional nodes make up for the lower centrifugal potential of states with lower l as compared to states with higher l. However, in atoms with more than one electron, orbitals with different values of l for a given value for n are not degenerate. In general ns has n-1 nodes, np n-2, nd n-3 etc. In hydrogen, all orbitals with the same principal quantum number 'n' (1,2,3.) are degenerate, regardless of the orbital angular momentum quantum number'l' (0,1.n-1 or s,p,d.). It states that Electrons will distribute themselves in. As per Hund’s rule, degenerate orbitals are filled evenly before electrons are filled into higher energy levels. In the case of filing of electrons into orbital having equal energies, called degenerate orbital. As per the Aufbau principle, lower energy levels are filled before higher energy levels. That is an example of degeneracy in an atomic system. The electrons in an atom are arranged in shells that surround the nucleus, with each successive shell being farther from the nucleus. To be more specific about the difference of radial functions for orbitals with different l, the 2s orbital has 1 radial node, 2p zero nodes. Degenerate orbitals definition: Electron orbitals having the same energy levels are called degenerate orbitals. Thus, the n=2 energy is said to be degenerate since an electron can have this energy and be in a multitude of different eigenstates of the system.
Any electron in the s orbital state or one of the p-orbital states will have this energy. Now, consider the n=2 energy for hydrogen. Thus, the n=1 energy is non degenerate since there is only one eigenstate the electron can be in (the s orbital) and have that energy. Similarly, in molecular orbital theory, latexsigma/latex orbitals are usually more stable than orbitals. There is only one orbital(eigenstate) which has the ground energy as an eigenvalue. As we saw in valence bond theory, latexsigma/latex bonds are generally more stable than latexpi/latex bonds formed from degenerate atomic orbitals. These orbitals are the eigenstates for the electron bound to the proton. In the H atom there are different energy levels and within each energy level you have an orbital corresponding to different allowed values for the electron's angular momentum. A given system is said to be degenerate if more than one eigenstate has the same energy as an eigenvalue. Your reasoning regarding the additional l-term in V eff(r) giving the Y lm(Ω) functions a different energy is not correct b/c different l-values also affect the R nl(r) functions.The concept of degeneracy is related to the energies of the different quantum states of a system. I am pretty sure that we had this disucussion here a couple of times. All these three orbitals have similar energy belonging to the same orbital (p), hence. The p orbital has three orbitals px, py, and pz. Example: An atom has four orbitals, namely s, p, d, and f. Just google for hydrogen atom SO(4) and you will find numerous articles, scripts and presentations. Here is a degenerate orbitals example that will help students to understand the degenerate orbital meaning more clearly. In this Chemistry video in Hindi for class 11 we explained energies of different atomic orbitals in single-electron atom/ions as well as in multi-electron a. The existence of the Laplace-Lenz-Runge vector and the l-degeneracy allowes one to solve the energy eigenvalue problem algebraically w/o solving the Schrödinger equation (W. The 1/r potential has not only the obvious SO(3) symmetry for spatial rotations but a larger SO(4) symmetry. the fact that E(n,l) = E(n) is l-independent is due to a hidden dynamical symmetry of the 1/r potential which results in an additional conserved quantity, the so-called Laplace-Lenz-Runge vector.


 0 kommentar(er)
0 kommentar(er)
